

The interesting thing is that both of us appear to be running into identical difficulties - it gets to a certain point where in order to continue, it seems imperative to come up with some clever transformation of the limit function. Jerome Keisler.Īfter discussing with Jad, conclusion is that the proof above is definitively not correct, specifically due to steps (4) and (7)!
Proof of mean value theorem using infinitesimals free#
One introduction to this subject is a free online book: “Elementary Calculus: An Approach Using Infinitesimals” by H.
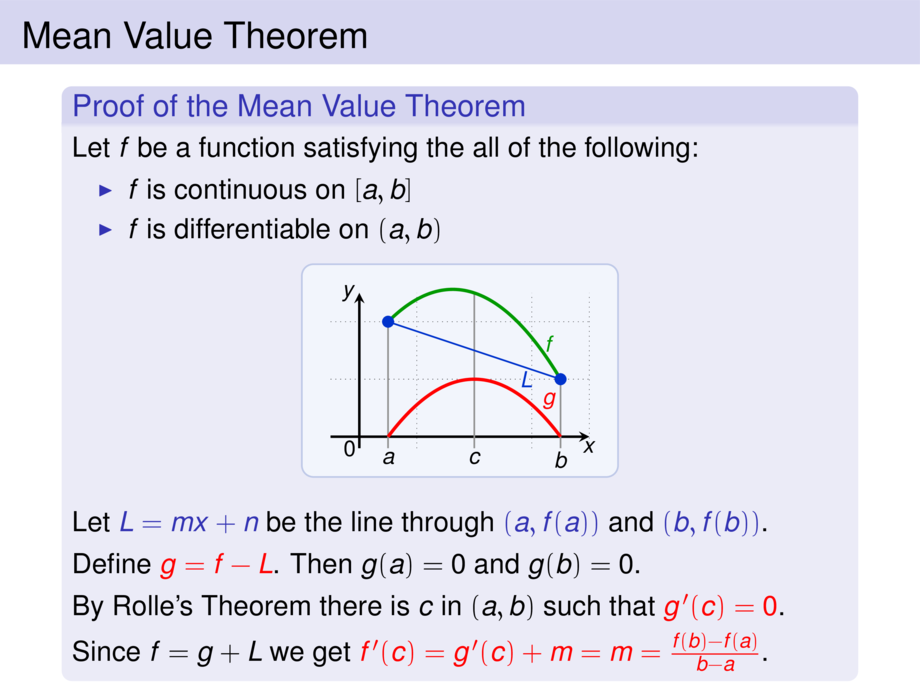
But it seems with a few definitions, you can have your cake Handwavy sloppy arguments that defied the rigour and precision thatĬenturies of mathematics fought for. Looked down on the pseudo-proofs I was shown in physics lectures, The notation is more elegant than those of limits. Inįact, not only is it possible, but it is quite easy to understand, and Methods that Newton and Leibniz first used when developing calculus. I only recently became aware that it is possible to formalize the Haven't had a chance to go over Jad's notes yet, but I intend to in next few days.įound this which I thought pretty interesting: onwards until he thinks he should stop, now this is I think is a very nice way to go about the proofs, it is not even necessarily harder than accepting caluclus, only more detailed, and in certain aspects.
5.5.52, As Tom pointed out this might be similar to what I was trying to prove earlier, but I have 2 thoughts:.I tried to think about this ignoring my doubts, but I failed 5.5.44 I am clueless, should not A depend on T as well, what does depreciation mean here? can we keep depreciating forever? if not when do we HAVE to overhaul? I don't get the model.5.5.43 I think the answer given is wrong! differentiating it does not produce f '.? I know cos(x2) does not because it was mentioned earlier, but still do I have to prove it? I tried a bit and failed.

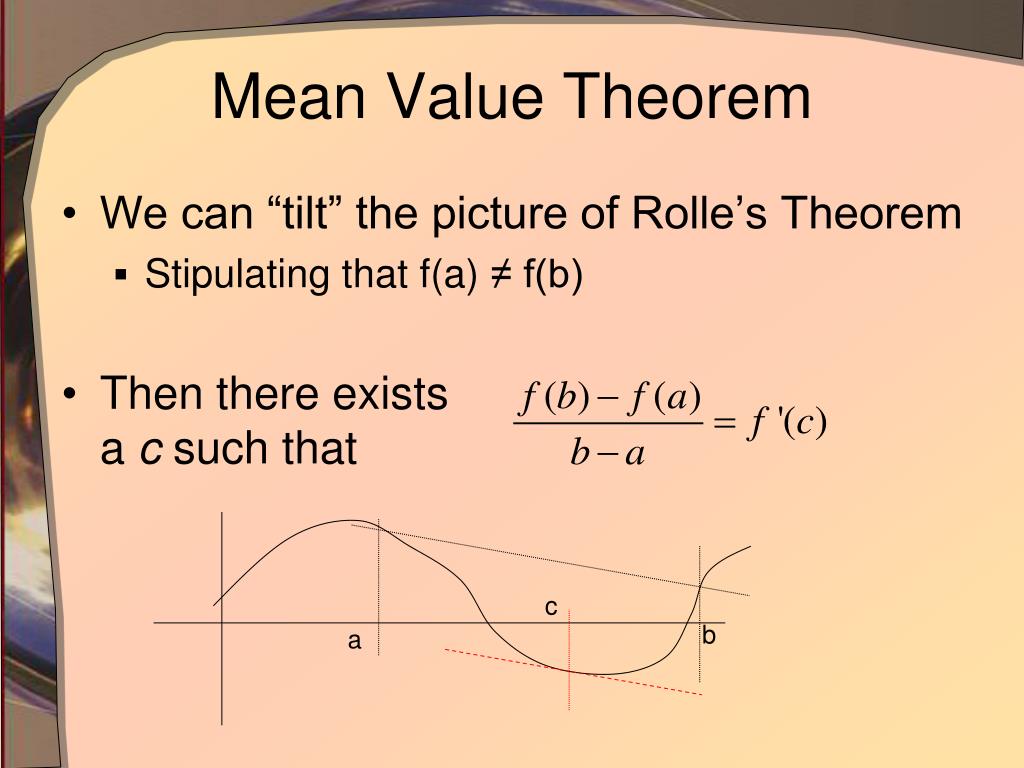
5.5.18, am I supposed to prove that sin (x2) has not antider.5.5.27 (and similar), does not the answer depend on x>17 and x, I found a better proof in notes 3, but I still want to see what I do not like about the proof in the book.It's not that any of the steps in Theorem 2a are technically incorrect, but they are starting off with the constant c on the outside of the integral?!?! WTF? , Theorem 2 (a), is that really a proof? We have proven that the derivatives of both sides are equal, does that mean the antiderivatives are? why? Wow, no that does NOT appear to be a proof.If you are still having trouble understanding the Mean Value theorem, then click on this link for a more detail explanation. Now that we have proved Rolle's theorem, then we can continue to prove the Mean Value theorem. Since we have proved all three cases, then we have just proved Rolle's theorem. In other words, there exists a number c such that a < c < b and f'(c) = 0. Since f'(x) exists and there is a minimum within the interval, then we know that f'(c) = 0 within. Since we know f(x) is differentiable, then we know that f'(x) exists. If f(x) is continuous, then that means there exists a minimum at point c. Case 3: Consider some number k in the interval such that f(k) Since f'(x) exists and there is a maximum within the interval, then we know that f'(c) = 0 within. If f(x) is continuous, then that means there exists a maximum at point c. Hence we found a number c such that a f(a) = f(b). Since f'(x) = 0 for all values of x, then we can choose any number within the interval as c.


 0 kommentar(er)
0 kommentar(er)
